Research.
My research program has two main pillars.
Last updated: Q3 2023.
- Theory of infinite-dimensional and/or non-smooth dynamical systems.
- Rigorous numerics and computer-assisted proof in dynamical systems.
Last updated: Q3 2023.
|
Infinite-dimensional and/or nonsooth dynamical systems.
Nonsmooth dynamical systems is a relatively new field whose development was motivated in part by its ubiquity in control engineering, but whose applications are now incredibly diverse. These systems spend most of their time evolving in a smooth manner, but under special circumstances their evolution can be interrupted in a discontinuous way. A simple example is a bouncing ball: it falls smoothly until it hits the ground, at which point its direction of travel is quickly reversed. From the perspective of simulation, such systems are more difficult to study with high precision because their structure frequently requires the numerical solver to be interrupted to either reset the state or verify zero-crossing conditions. These difficulties are further compounded if the continuous dynamics are governed by an infinite-dimensional dynamical system. Retarded functional differential equations -- RFDE for short -- are dynamical systems in which the immediate forward evolution depends explicitly on its prior history. These contrast to ordinary differential equations, for which the instantaneous rate of change depends only on the present state. The explicit way that the dynamics depend on the past often involve evaluations of the solution at delayed arguments, but they could also involve an integral term involving the history of the solution (a "distributed" delay). These equations are a natural setting to model phenomena in which there is a natural time lag, such as the incubation period of an infectious disease, a finite signal propagation time due to distance between sender and receiver, or the reaction of a control system to a user input. Some real-world systems involve events that occur infrequently but on very small time scales. It can sometimes be beneficial to model such events as occurring instantaneously -- that is, in zero time. If the system at hand also involves time lags, the result of such an approximation is an impulsive retarded functional differential equation (impulsive RFDE). They are a subclass of infinite-dimensional discontinuous dynamical systems. The interactions between delays and impulses can result in some surprising, non-classical bifurcation patterns and ill-conditioned initial-value problems. The theory of impulsive functional differential equations is still in development, particularly for state-dependent delays and systems with impulses triggered by state-dependent relationships. On the side of state-dependent delay alone, there are many as of yet unresolved problems concerning the regularity of the semiflow. |
Homotopy continuation of a closing-reopening cycle in a discontinuous infectious disease model with switching contact rate, motivated by the SARS-CoV-2 pandemic. Scale removed. Proven by computer-assisted proof.
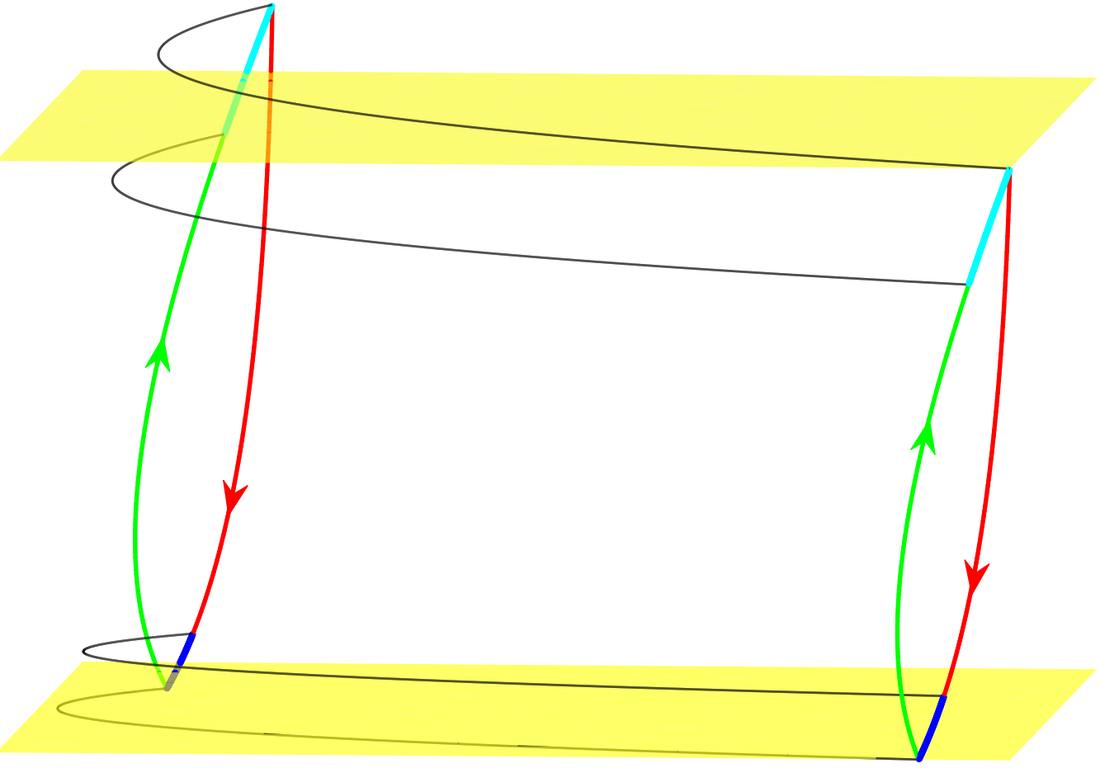
Plot of the quadratic coefficient of a (discontinuous) local centre manifold of a particular scalar impulsive delay differential equation. Time is on the horizontal axis, with history argument on the vertical axis. Discontinuities propagate with constant velocity; see the diagonal line between the blue and yellow regimes.
|
|
Rigorous numerics and computer-assisted proofs
Rigorously validated numerics, in a broad sense, concerns numerical methods that lead naturally to computer-assisted proofs for the existence of objects of relevance in dynamical systems and nonlinear analysis. It draws from techniques of nonlinear functional analysis and approximation theory to connect the existence of approximations of such invariant objects in a discretized model with an exact object in the original model. When analytical methods might not be helpful, rigorous numerics can at times fill in the gap. The applicability of these techniques is extremely broad. Some recent applications of independent interest include neural networks, cosmology and general relativity, and infectious disease modelling. In a more theoretical direction, rigorous numerics can reveal gaps in existing dynamical systems theories. For example, my recent work on state-dependent delay has suggests that theory for higher-regularity solution manifolds and semiflows must be developed, if the rigorous numerics for these systems is to truly flourish. |
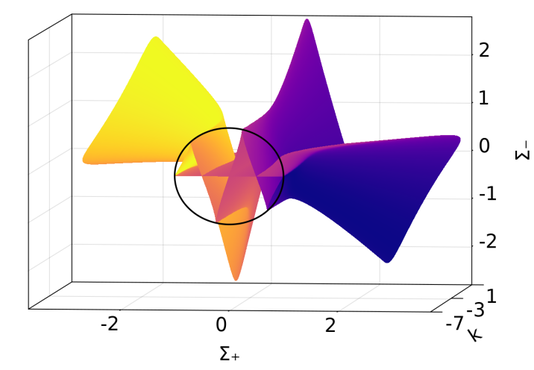
Continuation of Bianchi type IX periodic orbits in the extremal case (v=0) of spatially homogeneous Hořava-Lifshitz gravity, relative to the (black) Kasner circle of equilibria. The continuation parameter is a conserved quantity of the system. Orbits are proven (computer-assisted) at integer values of k.
|
|
Infectious disease modeling.
Nonsmooth dynamical systems ideas are very applicable to control, so it is natural that they have found use in infectious disease modeling. As for my own research, some recent project include The common thread here is that the lower order of smoothness in the model is due to a mechanism that controls the spread of the disease. Pandemic closing a reopening: In early 2020, the SARS-CoV-2 pandemic made it necessary for governments worldwide to impose lockdown conditions. This allowed us to collectively "flatten the curve", but was difficult for businesses and individuals. In spring and summer of that year, some amount of "reopening" allowed greater individual freedoms. This then caused further outbreaks and in the fall of 2020, many governments began lockdowns again. This "closing and reopening" can be modeled by relays. Here, the model involves a switching vector field, which is a type of discontinuous dynamical system. The discontinuity comes from lockdowns being imposed and lifted based on the progression of the pandemic, specifically a moving average of the number of active cases. The result is an implicitly-defined infinite-dimensional dynamical system. I completed the analysis of such a model, proving the existence of cycles with repeated closing and reopening events. Pulse vaccination with finite immunity: Pulse vaccination is a vaccination strategy whereby a large proportion of the population is vaccinated in a short period of time. This event is repeated after a set amount of time. It was unclear how effective such strategies are when the vaccine or clearance of the infection confers immunity for only a set amount of time. I analyzed a model that incorporated both of these effects. I found that if not enough people get vaccinated then smaller outbreaks may become more common year-round. These smaller outbreaks have a temporally quasiperiodic structure, so while they are oscillatory it is more difficult to anticipate them. |
Evolution of a cylindrical attractor with respect to vaccination efficacy in a time-delayed SIR model with pulse vaccination.
|
|
Neural networks.
Part 1: Control. Linear matrix inequalities (LMI) are indispensable tools in control theory and signal processing. Indeed, many solutions to classical control problems can be framed in terms of the existence of a solution to a LMI. When passing from a finite-dimensional problem like an ordinary differential equation in Euclidean space to a delay differential equation, however, even the problem of stabilizing an equilibrium becomes much more technical because of the infinitely many independent directions the state can travel, growing or decaying over time. Many authors have attempted to circumvent this problem by "projecting" the solution history into a finite-dimensional space, performing the control synthesis there using LMI methods, then attempting to reconstruct an appropriate controller for the infinite-dimensional system. Still other methods pose a stabilizing controller of a very specific form and verify that under certain LMI conditions, there is a Lyapunov functional that guarantees stability. A recent interest of mine has been in using invariant manifold data to guide control synthesis in stabilization problems for infinite-dimensional systems, and control of neural networks. The centre-unstable manifold of the given system can be used to derive a finite-dimensional dynamical system that faithfully captures the effect of introducing a small, perturbative controller on the "unstable part" of the system. The advantage of designing the controller with this method is that all of the well-behaved stable modes can be ignored, with the result being a controller that can be more conservative than one derived with a LMI applied to a lossy finite-dimensional projection. This method also avoids the need for a non-canonical projection onto a finite-dimensional system or the construction of a complicated Lyapunov functional. Moreover, the feasibility problem for impulsive stabilization can be effectively attacked using this idea. Part 2: Robustness. Modern advances in the training of neural networks have led to these techniques being used to develop controllers for physical systems, using unsupervised learning approaches. However, there are risks of this methodology that can be hidden by aggregate loss scores. Specifically, it can not account for variability in the (numerical, simulated) testing environment, and controllers trained this way can degrade substantially, to the point of being unsafe, on switching to an environment that is closer to reality. Our analysis was carried out on simple reinforcement learning benchmarks, with rigorous numerics as the proof methodology. Controller robustness is a broad topic, and as advances in artificial intelligence continue, it will become ever more important to have rigorous, exhaustive methods of testing controllers derived using AI. |
Top: Data buffer transient response in log-space in a theoretical computing system with error-prone workers after invariant manifold-guided stabilization. Bottom: convergence to steady state (workers individually coloured).
|
